Hamming code is one of the Computer Science/Telecommunication classics.
In this article, we’ll revisit the topic and implement a stateless Hamming encoder using Kotlin.
Hamming Error Correction
Our communication channels and data storage are error-prone – bits can flip due to various things like electric/magnetic interferences, background radiation, or just because of the low quality of materials used.
Since the neutron flux is ~300 higher at around 10km altitude, particular attention is necessary when dealing with systems operating at high altitudes – the case study of the Cassini-Huygens proves it – in space, a number of reported errors was over four times bigger than on earth, hence the need for efficient error correction.
Richard Hamming‘s Code is one of the solutions to the problem. It’s a perfect code (at least, according to Hamming’s definition) which can expose and correct errors in transmitted messages.
Simply put, it adds metadata to the message (in the form of parity bits) that can be used for validation and correction of errors in messages.
A Brief Explanation
I bet you already wondered what (7,4) in “Hamming(7,4)” means.
Simply put, N and M in “Hamming(N, M)” represent the block length and the message size – so, (7,4) means that it encodes four bits into seven bits by adding three(N-M) additional parity bits – as simple as that.
This particular version can detect and correct single-bit errors, and detect (but not correct) double-bit errors.
In Hamming’s codeword, parity bits always occupy all indexes that are powers of two (if we use 1-based-indexing to determine positions).
So, if our initial message is 1111, the codeword will look somewhat like [][]1[]111 – with three parity bits for us to fill in:
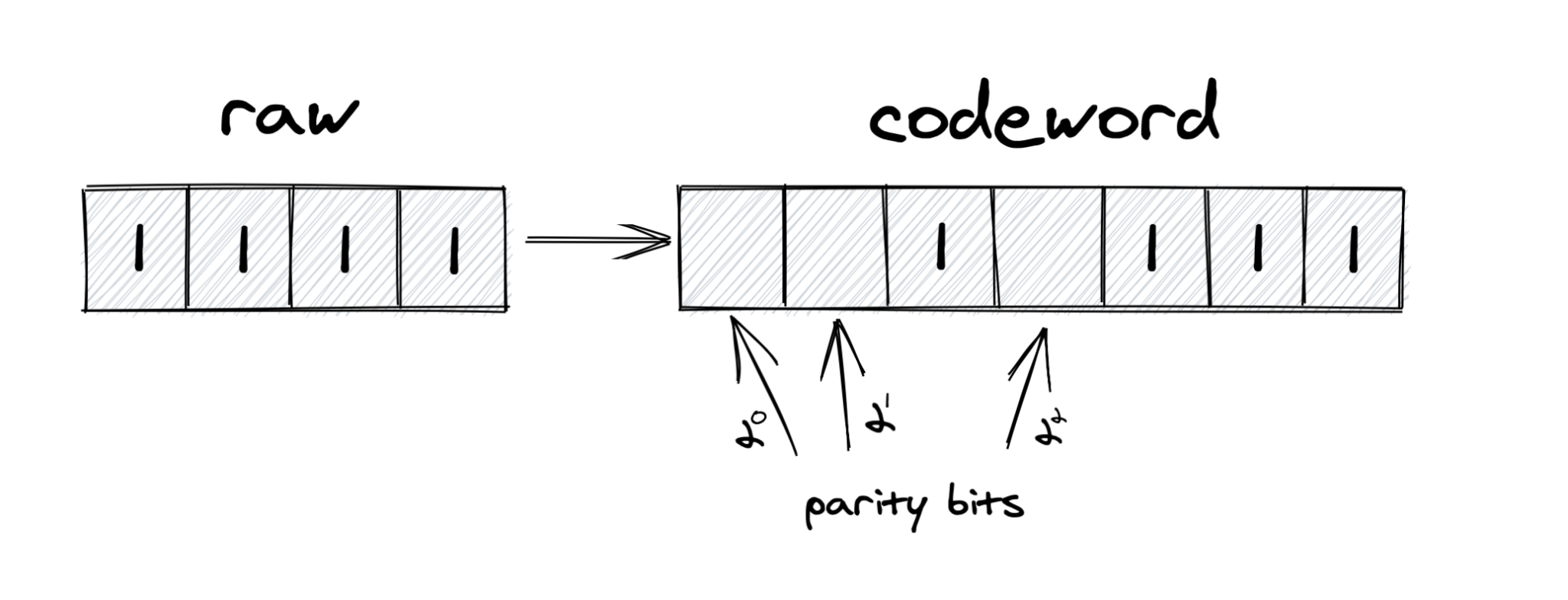
If we want to calculate the n-th parity bit, we start on its position in a codeword, we take n elements, skip n elements, take n elements, skip n elements… and so on. If the number of ones is odd, we set the parity bit to one, otherwise zero.
In our case:
- For the first parity bit, we check indexes 1,3,5,7 -> [1][]1[]111
- For the second parity bit, we check indexes 2,3,6,7 -> [1][1]1[]111
- For the third parity bit, we check indexes 4,5,6,7 -> [1][1]1[1]111
And that’s all – the codeword is 1111111.
In this case, it might be tempting to think that every sequence containing only ones will be encoded to another sequence comprising only ones… but that’s not the case… every message containing only zeros will always be encoded to zeros exclusively.
Encoding
First things first, we can leverage Type Driven Development to make our life easier when working with Strings representing raw and encoded messages:
data class EncodedString(val value: String) {
operator fun get(index: Int): Char = value[index]
val length get() = value.length
}
data class BinaryString(val value: String) {
operator fun get(index: Int): Char = value[index]
val length get() = value.length
}Using this approach, it’ll be slightly harder to mix them up. Additional delegated methods were added for the sake of convenience.
If we limited ourselves to 7-bit-long codewords, the implementation would not be super interesting – so we’ll go for the alternative that can adapt to the message length.
We’ll need a method for calculating the encoded codeword size for a given message. In this case, we simply find the lowest number of parity pairs that can cover the given message:
fun codewordSize(msgLength: Int) = generateSequence(2) { it + 1 }
.first { r -> msgLength + r + 1 <= (1 shl r) } + msgLengthNext, we’ll need a method for calculating parity and data bits at given indexes for a given message:
fun getParityBit(codeWordIndex: Int, msg: BinaryString) =
parityIndicesSequence(codeWordIndex, codewordSize(msg.value.length))
.map { getDataBit(it, msg).toInt() }
.reduce { a, b -> a xor b }
.toString()
fun getDataBit(ind: Int, input: BinaryString) = input
.value[ind - Integer.toBinaryString(ind).length].toString()Where parityIndicesSequence() is defined as:
fun parityIndicesSequence(start: Int, endEx: Int) = generateSequence(start) { it + 1 }
.take(endEx - start)
.filterIndexed { i, _ -> i % ((2 * (start + 1))) < start + 1 }
.drop(1) // ignore the initial parity bitNow, we can put it all together to form the actual solution, which simply is simply going through the whole codeword and filling it with parity bits and actual data:
override fun encode(input: BinaryString): EncodedString {
fun toHammingCodeValue(it: Int, input: BinaryString) =
when ((it + 1).isPowerOfTwo()) {
true -> hammingHelper.getParityBit(it, input)
false -> hammingHelper.getDataBit(it, input)
}
return hammingHelper.getHammingCodewordIndices(input.value.length)
.map { toHammingCodeValue(it, input) }
.joinToString("")
.let(::EncodedString)
}Note that isPowerOfTwo() is our custom extension function and is not available out-of-the-box in Kotlin:
internal fun Int.isPowerOfTwo() = this != 0 && this and this - 1 == 0
Inlined
The interesting thing is that the whole computation can be inlined to a single Goliath sequence:
override fun encode(input: BinaryString) = generateSequence(0) { it + 1 }
.take(generateSequence(2) { it + 1 }
.first { r -> input.value.length + r + 1 <= (1 shl r) } + input.value.length)
.map {
when ((it + 1).isPowerOfTwo()) {
true -> generateSequence(it) { it + 1 }
.take(generateSequence(2) { it + 1 }
.first { r -> input.value.length + r + 1 <= (1 shl r) } + input.value.length - it)
.filterIndexed { i, _ -> i % ((2 * (it + 1))) < it + 1 }
.drop(1)
.map {
input
.value[it - Integer.toBinaryString(it).length].toString().toInt()
}
.reduce { a, b -> a xor b }
.toString()
false -> input
.value[it - Integer.toBinaryString(it).length].toString()
}
}
.joinToString("")
.let(::EncodedString)Not the most readable version, but interesting to have a look.
In Action
We can verify that the implementation works as expected by leveraging JUnit5 and Parameterized Tests:
@ParameterizedTest(name = "{0} should be encoded to {1}")
@CsvSource(
"1,111",
"01,10011",
"11,01111",
"1001000,00110010000",
"1100001,10111001001",
"1101101,11101010101",
"1101001,01101011001",
"1101110,01101010110",
"1100111,01111001111",
"0100000,10011000000",
"1100011,11111000011",
"1101111,10101011111",
"1100100,11111001100",
"1100101,00111000101",
"10011010,011100101010")
fun shouldEncode(first: String, second: String) {
assertThat(sut.encode(BinaryString(first)))
.isEqualTo(EncodedString(second))
}… and by using a home-made property testing:
@Test
@DisplayName("should always encode zeros to zeros")
fun shouldEncodeZeros() {
generateSequence("0") { it + "0" }
.take(1000)
.map { sut.encode(BinaryString(it)).value }
.forEach {
assertThat(it).doesNotContain("1")
}
}Going Parallel
The most important property of this implementation is statelessness – it could be achieved by ensuring that we’re using only pure functions and avoiding shared mutable state – all necessary data is always passed explicitly as input parameters and not held in any form of internal state.
Unfortunately, it results in some repetition and performance overhead that could’ve been avoided if we’re just modifying one mutable list and passing it around… but now we can utilize our resources wiser by parallelizing the whole operation – which should result in performance improvement.
Without running the code, that’s just wishful thinking, so let’s do that.
We can parallelize the operation (naively) using Java 8’s parallel streams:
override fun encode(input: BinaryString) = hammingHelper.getHammingCodewordIndices(input.value.length)
.toList().parallelStream()
.map { toHammingCodeValue(it, input) }
.reduce("") { t, u -> t + u }
.let(::EncodedString)To not give the sequential implementation an unfair advantage (no toList() conversion so far), we’ll need to change the implementation slightly:
override fun encode(input: BinaryString) = hammingHelper.getHammingCodewordIndices(input.value.length)
.toList().stream() // to be fair.
.map { toHammingCodeValue(it, input) }
.reduce("") { t, u -> t + u }
.let(::EncodedString)And now, we can perform some benchmarking using JMH (message.size == 10_000):
Result "com.pivovarit.hamming.benchmarks.SimpleBenchmark.parallel": 3.690 ±(99.9%) 0.018 ms/op [Average] (min, avg, max) = (3.524, 3.690, 3.974), stdev = 0.076 CI (99.9%): [3.672, 3.708] (assumes normal distribution) Result "com.pivovarit.hamming.benchmarks.SimpleBenchmark.sequential": 10.877 ±(99.9%) 0.097 ms/op [Average] (min, avg, max) = (10.482, 10.877, 13.498), stdev = 0.410 CI (99.9%): [10.780, 10.974] (assumes normal distribution) # Run complete. Total time: 00:15:14 Benchmark Mode Cnt Score Error Units SimpleBenchmark.parallel avgt 200 3.690 ± 0.018 ms/op SimpleBenchmark.sequential avgt 200 10.877 ± 0.097 ms/op
As we can see, we can notice a major performance improvement in favour of the parallelized implementation – of course; results might drastically change because of various factors, so do not think that we’ve found a silver bullet – they do not exist.
For example, here are the results for encoding a very short message (message.size == 10)):
Benchmark Mode Cnt Score Error Units SimpleBenchmark.parallel avgt 200 0.024 ± 0.001 ms/op SimpleBenchmark.sequential avgt 200 0.003 ± 0.001 ms/op
In this case, the overhead of splitting the operation among multiple threads makes the parallelized implementation perform eight times slower(sic!).
Here’s the full table for the reference:
Benchmark (messageSize) Mode Cnt Score Error Units Benchmark.parallel 10 avgt 200 0.022 ± 0.001 ms/op Benchmark.sequential 10 avgt 200 0.003 ± 0.001 ms/op Benchmark.parallel 100 avgt 200 0.038 ± 0.001 ms/op Benchmark.sequential 100 avgt 200 0.031 ± 0.001 ms/op Benchmark.parallel 1000 avgt 200 0.273 ± 0.011 ms/op Benchmark.sequential 1000 avgt 200 0.470 ± 0.008 ms/op Benchmark.parallel 10000 avgt 200 3.731 ± 0.047 ms/op Benchmark.sequential 10000 avgt 200 12.425 ± 0.336 ms/op
Conclusion
We saw how to implement a thread-safe Hamming encoder using Kotlin and what parallelization can potentially give us.
In the second part of the article, we’ll implement a Hamming decoder and see how we can correct single-bit errors and detect double-bit ones.
Code snippets can be found on GitHub.



